In a previous post, we discussed the process of calculating interrater reliability (IRR) on qualitatively coded data using Cohen’s kappa. However, there are many different tests that can be used to calculate IRR, depending on the type of qualitative coding that you have done. In this post, I will discuss using Fleiss’ kappa, including when it should be used and how to calculate it.
As explained in the previous post, one method of analyzing qualitative data is by developing a codebook, which contains all the possible codes raters could use. However, it is important to know how well your raters agreed on the codes they assigned to the data to identify if disagreements were from conceptual disagreements on what the codes mean or from subjective disagreements. These types of disagreements could mean that the qualitative coding process is not robust, or that the coders have not applied it similarly, and could affect the quality of the research data. Therefore, it is important to calculate IRR to understand the degree of disagreement between raters for a set of qualitative data [1].
Fleiss’ kappa is an extension of Cohen’s kappa, both used to calculate IRR. Cohen’s kappa finds the IRR between two raters for one specific code. Fleiss’ kappa is Cohen’s kappa modified for more than two raters for all the codes used [2]. While Cohen’s kappa can be used for more than two raters, it is a little more complex to do so. Researchers would have to calculate Cohen’s kappa between each pair of raters for each possible code and then calculate the average of those kappa values to find an IRR. Fleiss’ kappa shortens this process by calculating a single kappa for all the raters for all possible combinations of codes. This single kappa is the IRR. Fleiss’ kappa can also be used when raters have coded a different number of responses, if each response is coded by the same number of raters. Cohen’s kappa does not allow this [3].
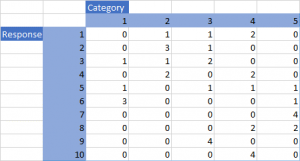
To calculate Fleiss’ kappa, a table should be created where the top row contains all the codes and combinations of codes, called categories, that raters used. The left most column represents the qualitative data being coded. Each row indicates what category was chosen by the raters for that response. This means that each row should total to the number of raters. Table 1 shows an example of how the data should be represented in such a table, with 10 responses being coded into 5 categories by 4 raters.
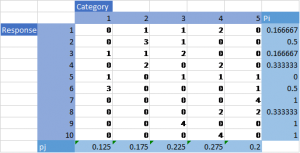
Now that the data is set up, we can start the Fleiss’ kappa calculations. It is important to keep track of the number of raters, n, and the number of responses, N. For each row, we must calculate how many rater pairs agreed, relative to the number of all possible pairs. This is Pi, which is every number in the row squared subtracted by n and divided by n(n-1) [4]. Next, we must calculate the proportion of all assignments, pj, for each category. For each column, pj is the sum of the column divided by n*N [4].
Using these Pi and pj values, the observed and expected agreements can now be calculated. The observed agreement is the sum of all the Pi values divided by the number of responses being coded [4]. The expected agreement is the sum of each pj value squared [4]. This means that for our example, our observed agreement is 0.5 while our expected agreement is 0.2125.
Using these observed and expected agreements, we can calculate Fleiss’ kappa, which uses the same formula as Cohen’s kappa, where kappa is:
(observed agreement) – (expected agreement) / (1 – (expected agreement))
[4]. This means the IRR for our example is 0.365.
The following table can be used to interpret the IRR [5]:
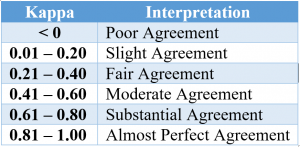
Our project initially was using the simpler Cohen’s kappa calculation, which was extremely helpful in understanding the general subject of IRR. Learning Fleiss’ kappa has helped our current project immensely, though, because we have more than two raters, and using Fleiss’ kappa is a better approach in this case.
As a third-year undergraduate student majoring in Computer Engineering, I have learned a lot about the world of research and data analysis during my time at the INIT Lab. Learning both Cohen’s and Fleiss’ kappa has helped me understand that there is more than one way of finding an IRR and has helped me better understand the degrees of agreement between raters. By learning these subjects, I am now better at recognizing what method of IRR calculation is best to use and if a published paper used a valid method to do so.
REFERENCES
- Gwet, K. L. (2014). Handbook of inter-rater reliability: The definitive guide to measuring the extent of agreement among raters. Advanced Analytics, LLC.
- McHugh M. L. (). Interrater reliability: the kappa statistic. Biochemia medica, 22(3), 276–282.
- Fleiss, J. L. (1971) “Measuring nominal scale agreement among many raters.” Psychological Bulletin, Vol. 76, No. 5 pp. 378–382
- Banerjee, M., Capozzoli, M., McSweeney, L., & Sinha, D. (1999). Beyond kappa: A review of interrater agreement measures. Canadian journal of statistics, 27(1), 3-23.
- Landis, J. R. and Koch, G. G. (1977) “The measurement of observer agreement for categorical data” in Biometrics. Vol. 33, pp. 159–174